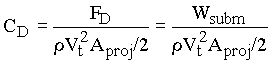![]()
![]()
The primary purpose of this laboratory experiment is to see the application of dimensional analysis to obtain dimensionless parameters that reduce the number of variables needed to represent a physical process. The physical process in this laboratory experiment is the drag (resistance) force on spheres moving through a fluid.
In the experiments, the rate at which spheres fall through liquids will be measured. Using dimensional analysis, the results apply equally well to spheres falling through gases instead of liquids or light spheres rising through gases or liquids. The results of these experiments and any others should be used only within the same range of dimensionless variables for which the tests are done.
The Theory section summarizes some concepts of objects moving through fluids. These flows are sometimes called external flows, since the fluid is outside of the object. Internal flows are flows in pipes and ducts.
![]()
The drag force (FD) on a submerged spherical object is dependent on the diameter of the sphere (D), the relative velocity between the sphere and the fluid (V), the fluid density (r), and the fluid viscosity (m). In other words, FD = f(D, V, r, m), where f indicates a functional relationship, which just gives another way of saying that FD depends on D, V, r, and m. The dimensions (indicated by the square brackets) of each variable are as follows:
Since there are 5 dimensional variables and 3 dimensions, there are two dimensionless variables for this problem. The units can be canceled in steps, beginning with the parameter which has the largest number of dimensions. In this case, the process will begin with the drag force, which has the largest number of dimensions when expressed in terms of mass. First divide the force by the density to cancel the mass dimension:
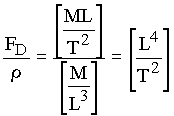
Since T2 is in the denominator, divide by V2 to cancel the time dimension:
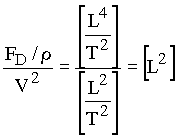
Finally, divide by D2 to cancel the length dimension:
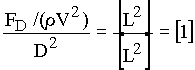
Since the result is dimensionless, the first dimensionless variable is
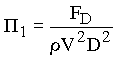
To be certain that the second dimensionless parameter is independent of the first one, the same process can be done again beginning with one of the dimensional variables which is not in the first dimensionless parameter and which has the largest number of dimensions. Thus, start with m since it is the only parameter not in the first dimensionless term (and since it contains all of the dimensions). Divide by r to cancel the mass dimension:
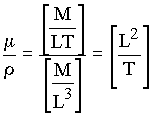
Since T is in the denominator, divide by V to cancel the time dimension:
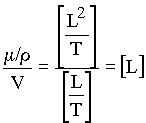
Finally divide by D to cancel the remaining length dimension:
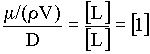
Since this result is dimensionless, the second dimensionless variable is
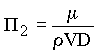
From the original relation and the two dimensionless parameters,
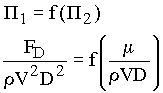
It can be confirmed that these two parameters are indeed dimensionless by inserting the dimensions for each term and seeing that all of the dimensions cancel.
There are some dimensionless groups that occur frequently in fluid mechanics and thus have evolved into standard forms. In this case, P1 is similar to a parameter called a drag coefficient (CD), where
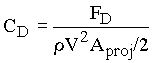
Aproj is the projected area, i.e., the area of the object projected onto a plane perpendicular to the flow so that Aproj = pD2/4 for a sphere. Comparison with P1 will show that CD = 8P1/p. The general functional dependence, namely P1 = f(P2), is not changed by constant factors.
P2 is the inverse of a dimensionless parameter called the Reynold's number and abbreviated as Re:
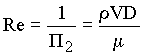
The Reynold's number can be interpreted as the ratio of inertial forces to viscous forces.
The general functional dependence is not changed by constant factors or by combining or inverting parameters as long as the proper number of independent, dimensionless parameters is maintained. Thus, the original relation P1 = f(P2) can be written as CD = f(Re). The functional relationship originally represented by 5 variables is now totally representated by only two variables.
The settling of a particle in a fluid can be analyzed by the classic laws of sedimentation formulated by Newton and Stokes. Newton's law yields the terminal particle velocity, which is the steady velocity that an object has when its submerged weight is equal to the resistance or drag force exerted by the fluid. At the terminal velocity (Vt), the sum of the forces is zero so there is no acceleration and the velocity is constant. An object's submerged weight (Wsubm) is its weight (Ws) minus the buoyant force (FB). The submerged will be upward if the buoyant force is greater than the weight. The terminal velocity can be found by equating the submerged weight of an object with the drag force (FD), i.e.,
drag force = submerged weight = weight - buoyant force
FD = Wsubm = Ws - FB
The weight (Ws) of an object with a constant density is
Ws = rsg"s
where rs = the density of the particle, g = the
acceleration due to gravity, and "s = the
volume of the particle. For a spherical particle, this volume is
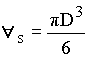
If the object is displacing fluid with a constant density, the buoyant force is
FB = rg"s
where r = the density of the fluid. The submerged weight (Wsubm) is then WB = (rs - r)g"s.
The drag force can be written as
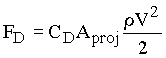
where CD is a drag coefficient. Equating the submerged weight and the
drag force yields
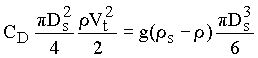
where Vt is the terminal velocity. Solving for the velocity yields
Newton's law for terminal velocity, which is
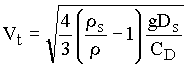
The drag coefficient has different values depending on whether the flow surrounding the
particle is laminar or turbulent (i.e., depending on the value of Re). For smooth,
spherical particles with Re < 1000, the drag coefficient can be approximated by
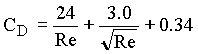
This relationship between the drag coefficient and Reynold's number for smooth spheres is shown below.
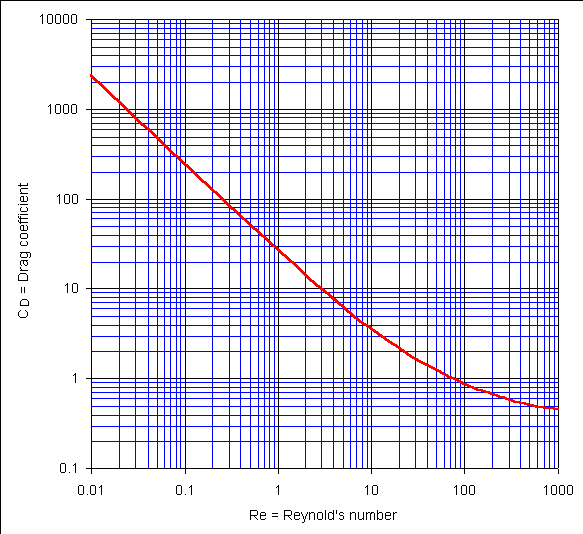
Drag Coefficients for Smooth Spheres
For Reynold's numbers less than about 0.5, the flow is called a creeping flow.
The accelerations (inertial forces) of the fluid particles around the object are so small
that they are insignificant. The first term dominates the equation, so CD
= 24/Re. Substituting this value into Newton's law yields Stoke's law for terminal
velocity for Re < 0.5, namely,
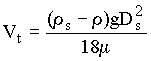
![]()
The apparatus consists of three cylindrical tubes, each containing a different liquid. The density and viscosity of each liquid are known. There are also spheres of known diameter and specific weight.
![]()